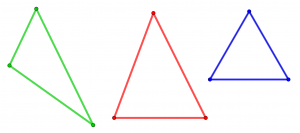
Glede na dolžino stranic ločimo:
- raznostranične trikotnike (vse stranice so različno dolge),
- enakokrake trikotnike (obstajata enako dolgi stranici),
- enakostranične trikotnike (vse stranice so enako dolge).
Velja, da je vsak enakostranični trikotnik tudi enakokrak. Ne velja, da je enakokrak trikotnik tudi enakostranični.
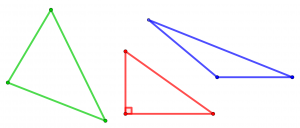
Glede na velikost notranjih kotov ločimo:
- ostrokotne trikotnike (trije ostri notranji koti),
- pravokotne trikotnike (en notranji kot je pravi kot, ki meri 90° ),
- topokotne trikotnike (en notranji kot je topi kot).
Lastnosti pravokotnega trikotnika (na zgornji sliki je narisan z rdečo barvo):
- en notranji kot meri 90°
- stranice imajo posebna imena:
- najdaljša stranica, ki leži nasproti pravega kota, se imenuje hipotenuza
- obe krajši stranici, ki oklepata pravi kot, se imenujeta kateti
V pravokotnem trikotniku velja Pitagorov izrek, ki pravi, da je ploščina kvadrata nad hipotenuzo enaka vsoti ploščin kvadratov nad obema katetama. S formulo ga ponazorimo tako: c2 = a2 + b2, kjer sta a in b dolžini stranic obeh katet, c pa je dolžina hipotenuze pravokotnega trikotnika.
Pomni: Pitagorov izrek velja le za pravokotni trikotnik.
Za boljšo prestavo si oglej naslednji video posnetek, ki ponazarja Pitagorov izrek.
S pomočjo spodnjega programa premikaj točke in preoblikuj trikotnik v vse zgoraj naštete oblike trikotnokov: