Razdalja od točke do premice
RAZDALJA MED TOČKAMA NA ŠTEVILSKI PREMICI
Namen: Ponovil boš, kako določiš razdaljo med točkama na številski premici.
OZNAKA: d (A,B) = |0 – (-3)| = |0 + 3| = 3
SPLOŠNO: d (A,B) = |b – a|

NAVODILA
Naloge preveriš s klikom na posamezen primer.
(B, C)
d (B, C) = |4 – 0| = 4
(C, D)
d (C, D) = |6 – 4| = 2
(A, C)
d (A, C) = |4 – (-3)| = |4 + 3| = 7
RAZDALJA TOČKE OD PREMICE
Namen: Ponovil boš, kako določiš razdaljo med točko in premico.
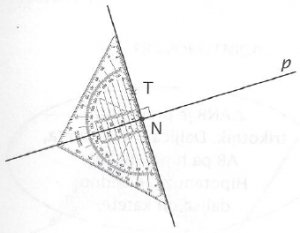
Postopek merjenja razdalje točke od premice:
- pravokotnica na premico skozi točko
- oznaka pravega kota in nožišča N
- imerjenje razdalje med točko in točko N
- zapis razdalje
Kako zapišem izmerjeno razdaljo?
OZNAKA: d (A, p) = 5,6 cm
Preberem: “Razdalja med točko A in premico p meri 5,6 centimetrov.”
PITAGOROV IZREK
Namen: Ponovil boš Pitagorov izrek.
Lastnosti pravokotnega trikotnika:
- en notranji kot meri 90°
- stranice imajo posebna imena:
- najdaljša stranica, ki leži nasproti pravega kota, se imenuje hipotenuza
- obe krajši stranici, ki oklepata pravi kot, se imenujeta kateti
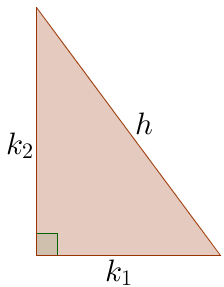
Pitagorov izrek (velja v pravokotnem trikotniku):
c2 = a2 + b2
c … hipotenuza
a … kateta
b … kateta
Ploščina kvadrata nad hipotenuzo je enaka vsoti ploščin kvadratov nad obema katetama.